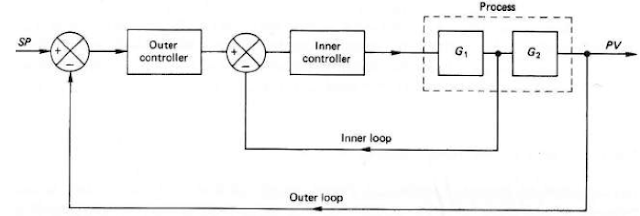
In General Navigation, when talking about position fixes,
one can differentiate between: Rho-Rho, Rho-Theta and Theta-Theta position
determination types. The importance of this kind of position fixing have
evolved with the appearance of a distance measuring equipment (DME)-based
aircraft navigation techniques (DME/DME). The newly developing system is
overtaking the GNSS in the next decade due to the GNSS’s weak signal and possible
disruption disadvantage. To start with the basics, one can define Rho as a
Greek letter R, which stands for range. Theta is an angle, thus a Rho-Rho fix
is made from two ranges, a Rho-Theta fix is a fix made from an angle and so on.
Rho-Rho method:
The goal of the position determination with the Rho-Rho
method is to find the aircraft’s position in 2D coordinate system, with the
help of beacon’s in the range of their signal. The R-R technique requires only
two range/distance measurements for a fix. [1]
 To have a sufficiently correct and acceptable
position, at least two beacon’s signal is needed to be located. The circle of
the two will define two points in space (Figure 1.) but only one of them is
showing the true position of the aircraft. In reality, if the aircraft is
flying from a departing city to a destination, with a given heading, it is
obvious which of these two points is determining the actual position of the
aircraft. In other, uncertain situations this can be also resolved by tuning
into a third DME or tuning into a VOR station. [2]
To have a sufficiently correct and acceptable
position, at least two beacon’s signal is needed to be located. The circle of
the two will define two points in space (Figure 1.) but only one of them is
showing the true position of the aircraft. In reality, if the aircraft is
flying from a departing city to a destination, with a given heading, it is
obvious which of these two points is determining the actual position of the
aircraft. In other, uncertain situations this can be also resolved by tuning
into a third DME or tuning into a VOR station. [2] |
| Ambiguity of DME position fix |
The R-R method works the best for incoming signals perpendicularly
to each other, and has the biggest error, if aligned in a line. This is
illustrated by the following figures.
 |
| Beacons are displaced with right angle relative to each other |
 |
| Beacons are displaced almost in line, highest error |
It is also important to note that reliability problems
may occur when using the R-R method for navigation in the vicinity of the
airport at low altitudes, due to the line of sight problem.
Defining the expression: Dilution of Precision (DOP)
will determine this reliability problem. It is an error occurring in all
positioning systems. Since, each position line is subjected to errors, the DOP
encounters only the influence of the geometry.
Rho-Rho-Rho method:
By having 3 range measurements from 3 different sources
(satellites for GPS), we can determine also 2D position. (To have 3D position,
4 satellites are necessary)
Illustration of this kind of position fix is shown on the
next figure.
In an RNAV mode using multiple DME, inaccuracy can be due
to inability to confirm that the aircraft is within the Designated Operational Coverage (DOC) area of the DMEs because of
identification problems.
Rho-Theta method:
VOR/DME position fixing is a typical example, used in VOR/DME-based
Area Navigation System. The VOR/DME Area Navigation system has its own VHF NAV
tuner and the system itself tunes the DME stations providing the best angular
position lines. (When operating in the dead reckoning mode, data used are: TAS from the Air Data Computer; heading
from the aircraft compass; the last computed W/V.) In a VOR/DME-based Area
Navigation System, the crosstrack distance, alongtrack distance and angular
course deviation information are provided.
One of the functions of the computer in a basic RNAV
system is to transfer the information given by a VOR/DME station into tracking
and distance indications to any chosen Phantom Station/waypoint. A "phantom
station" is created by setting the distance (Rho) and the bearing
(Theta) of the waypoint from a convenient VORTAC in the appropriate windows of
the waypoint selector. A series of these "phantom stations" or
waypoints make up an RNAV route.
 |
| Illustration of a phantom station [EASA] |
Theta-Theta method:
Intersection from two VOR bearings:
To sum it up, in an RNAV system, the Rho-Rho combination
of external reference will give the most accurate position. Rho is the Greek
letter ρ, which stands for range. Θ Theta is an angle. Thus a Rho-Rho fix is made
from two ranges (e.g. DME/DME) and a Rho-Theta fix is a fix made from a range
and an angle (e.g. VOR/DME).
- R-R uses distance/range from two sources for position determination,
- R-T uses VOR/DME for position determination,
- T-T uses bearings from two VOR stations.
Sources:
Picture references: Attitude and Navigation
Systems, Lecture notes, Warsaw University of Technology, www.daas.meil.pw.edu
[1] - Myron Kayton, Walter R. Fried, Avionics Navigation
Systems, pp.164.
[2] - David
Wyatt, Mike Tooley, Aircraft Communications and Navigation Systems, 2007