In this post, you can see how the
analysis of the accuracy of the given finite-difference formula is achieved for
a first order derivative case.
In order to solve ODE problems or Partial Differential
Equations (PDE) by system of algebraic equations, there are certain methods
available. The Finite Difference method is probably the oldest numerical method
that is used.
 |
| Figure 1. Numerical solution flowchart |
It is recommended to choose a
uniformly distributed grid size, having the size of X and Y components the
same, due to memory limitations.
Suppose that function U(x) is given as
such:
 |
| Figure 2. Selection of points on a function |
One would like to estimate the first derivative
of the function U(x) at some point x(j). The value of the
neighboring nodes are given: uj = u(xj), uj+1,
uj-1, where xj = j*h.
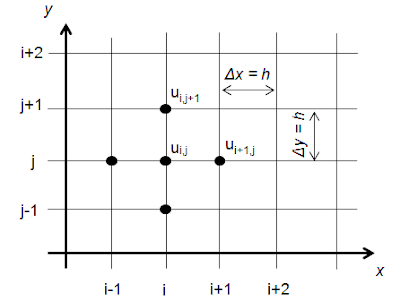 |
| Figure 3. 2D final difference grid |
Having a differential equation for a 2D,
compressible flow, non-viscous, non-stationary:
One takes the definition of the first
derivative:
If the discretization is small enough
(Δx), it will approximate the value of the function as:
Similarly to Equation (1.2) one can propose
different algebraic formulas for determining the determinant for a given point
of the function.
It is important to notice that Equations (1.2) and
(1.4) are 1st order accurate, meanwhile (1.5) is 2nd
order accurate.
 |
| Figure 4. Different approximations |
From the above plot, it is clearly
visible that out of the 3 different formulas for finding the derivative at a
given point Xj, the line that is closest to the tangent point at that point is
III. This is the so called central
difference and is more accurate that the other, forward difference one. The
errors can be determined simply by the Taylor expansion.
Similarly to Equation (1.3) the
following algebraic equations can be written:
One can conclude that the finite
difference formula has order of accuracy n and is proportional to hn for small values of step
size h. The central difference is 2nd order accurate and higher
order terms are resulting in lower accuracy, therefore the 2nd order
formula works best for calculating ODE-s and PDE-s.
Other method for deriving finite
difference formulas (with different accuracy) for a given differential order
remains a problem to solve.
To download full text in PDF: click here
Reference: Computational Fluid Dynamics, Lecture notes - Jacek Rokicki, 2014

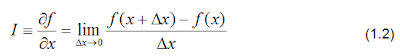



No comments:
Post a Comment